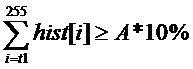图像处理二之----摄像头二值化算法汇总+代码

上一节中我们讲解了什么是二值化，并且讲到了二值化的一般方法，那么每种算法究竟是怎么样对图像经行二值化处理的呢？，算法的原理是什么呢，怎么样用代码实现，这节我们分享下。

1.otsu（最大类间方差法、大津法）

最大类间方差法是由日本学者大津于1979年提出的,是一种自适应的阈值确定的方法,又叫大津法,简称OTSU。它是按图像的灰度特性,将图像分成背景和目标2部分。背景和目标之间的类间方差越大,说明构成图像的2部分的差别越大,当部分目标错分为背景或部分背景错分为目标都会导致2部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。

阈值将原图象分成前景，背景两个图象。

当取最佳阈值时，背景应该与前景差别最大，关键在于如何选择衡量差别的标准

而在otsu算法中这个衡量差别的标准就是最大类间方差（英文简称otsu，这也就是这个算法名字的来源）

对于图像I(x,y),前景(即目标)和背景的分割阈值记作T,前景图像占整幅图像的比例记为ω0,其平均灰度μ0;背景图像占整幅图像的比例为ω1,其平均灰度为μ1。图像的总平均灰度记为μ,类间方差记为g。M×N = 像素总数,图像中像素的灰度值小于阈值T的像素个数记作N0,像素灰度大于阈值T的像素个数记作N1

,则有:
　　前景图像占比　　　　ω0=N0/ M×N (1)
　　背景图像占比　　　　ω1=N1/ M×N (2)
　　前景像素+背景像素　　　 N0+N1=M×N (3)
　　背景图像+前景图像占比　　　 　ω0+ω1=1 （4)
　　0~M灰度区间的灰度累计值　　 (5)

　 类间方差值　　　 (6)

将式(5)代入式(6),得到等价公式:
(7)

或

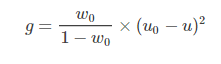
采用遍历的方法得到使类间方差最大的阈值T,即为所求。

代码实现：

c代码

w0为背景像素点占整幅图像的比例

u0为w0平均灰度

w1为前景像素点占整幅图像的比例

u1为w1平均灰度

u为整幅图像的平均灰度

类间方差公式 g = w1 * w2 * (u1 - u2) ^ 2int otsuThreshold(int *image, int col, int row)
{
    #define GrayScale 256
    int width = col;    int height = row;    int pixelCount\[GrayScale\] = {0}; //每个灰度值所占像素个数
    float pixelPro\[GrayScale\] = {0};//每个灰度值所占总像素比例
    int i, j, pixelSum = width * height;   //总像素
    int threshold = 0;    int* data = image;  //指向像素数据的指针


    //统计灰度级中每个像素在整幅图像中的个数  
    for (i = 0; i < height; i++)
    {        for (j = 0; j < width; j++)
        {
            pixelCount\[(int)data\[i * width + j\]\]++;  //将像素值作为计数数组的下标
        }
    }    //遍历灰度级\[0,255\]  
    float w0, w1, u0tmp, u1tmp, u0, u1, u, deltaTmp, deltaMax = 0;    for (i = 0; i < GrayScale; i++)     // i作为阈值
    {
        w0 = w1 = u0tmp = u1tmp = u0 = u1 = u = deltaTmp = 0;        for (j = 0; j < GrayScale; j++)
        {            if (j <= i)   //背景部分  
            {
                pixelPro\[i\] = (float)pixelCount\[i\] / pixelSum;   //计算每个像素在整幅图像中的比例  
                w0 += pixelPro\[j\];//背景像素点占整个图像的比例
                u0tmp += j * pixelPro\[j\];
            }            else   //前景部分  
            {
                pixelPro\[i\] = (float)pixelCount\[i\] / pixelSum;   //计算每个像素在整幅图像中的比例  
                w1 += pixelPro\[j\];//前景像素点占整个图像的比例
                u1tmp += j * pixelPro\[j\];
            }
        }
        u0 = u0tmp / w0;//背景平均灰度μ0
        u1 = u1tmp / w1;//前景平均灰度μ1
        deltaTmp = (float)(w0 \*w1\* pow((u0 - u1), 2)); //类间方差公式 g = w1 * w2 * (u1 - u2) ^ 2
        if (deltaTmp > deltaMax)
        {
            deltaMax = deltaTmp;
            threshold = i;
        }
    }    return threshold;
    
}

MATALB代码：

close all;
clear all;
clc;

input = imread('R.png');%读图
input = rgb2gray(input);%灰度转换

L = 256;%给定灰度级
\[ni, li\] = imhist(input,L);  %ni-各灰度等级出现的次数；li-对应的各灰度等级
% figure,plot(xi,ni);%显示绝对直方图统计
% title('绝对直方图统计')

\[M,N\] = size(input);%获取图像大小
MN = M*N;%像素点总数

%%Step1 计算归一化直方图

pi = ni/MN;  %pi-统计各灰度级出现的概率
figure,plot(li,pi);%显示相对直方图统计
title('相对直方图统计')

%%Step2  计算像素被分到C1中的概率P1(k)

sum = 0;%用来存储各灰度级概率和
P1 = zeros(L,1);%用来存储累积概率和for k = 1:L
    sum = sum +pi(k,1);
    P1(k,1) = sum;%累加概率
end

%%Step3  计算像素至K级的累积均值m(k)

sum1 = 0;%用来存储灰度均值
m = zeros(L,1);%用来存储累计均值for k = 1:L
    sum1 = sum1+k*pi(k,1);
    m(k,1) = sum1;%累积均值
end

%%Step4  计算全局灰度均值mg

mg = sum1;

%%Step5 计算类间方差sigmaB2 
sigmaB2 = zeros(L,1);for k = 1:L    if(P1(k,1) == 0)
        sigmaB2(k,1) = 0;  %为了防止出现NaN    else
        sigmaB2(k,1) = ((mg\*P1(k,1)-m(k,1))^2)/(P1(k,1)\*(1-P1(k,1)));
    end
end

%%Step6 得到最大类间方差以及阈值

\[MsigmaB2,T\] = max(sigmaB2);%获取最大类间方差MsigmaB2，以及所在位置（即阈值）
output = zeros(M,N);%定义二值化输出图像for i = 1:M    for j = 1:N        if input(i,j)>T
            output(i,j) = 1;        else
            output(i,j)=0;
        end
    end
end
figure,imshow(output);%显示结果

%%Step7 可分性度量eta

sigmaG2 = 0;%全局方差for k = 1:L
    sigmaG2 = sigmaG2+(k-mg)^2*pi(k,1);
end
eta = MsigmaB2/sigmaG2;

或者直接调用MATALB函数

I=imread('D:\\Images\\pic_loc\\1870405130305041503.jpg');
a=rgb2gray(I);
level = graythresh(a);
a=im2bw(a,level);
imshow(a,\[\]);

缺陷:OSTU算法在处理光照不均匀的图像的时候，效果会明显不好，因为利用的是全局像素信息。

2.灰度平局值法：

　**　1、描述:即使用整幅图像的灰度平均值作为二值化的阈值，一般该方法可作为其他方法的初始猜想值。**

原理：

代码实现：

 public static int GetMeanThreshold(int* HistGram)
    {        int Sum = 0, Amount = 0;        for (int Y = 0; Y < 256; Y++)
        {
            Amount += HistGram\[Y\];
            Sum += Y * HistGram\[Y\];
        }        return Sum / Amount;
    }

缺点：同样受光线影响较大，但是方法简单，处理快

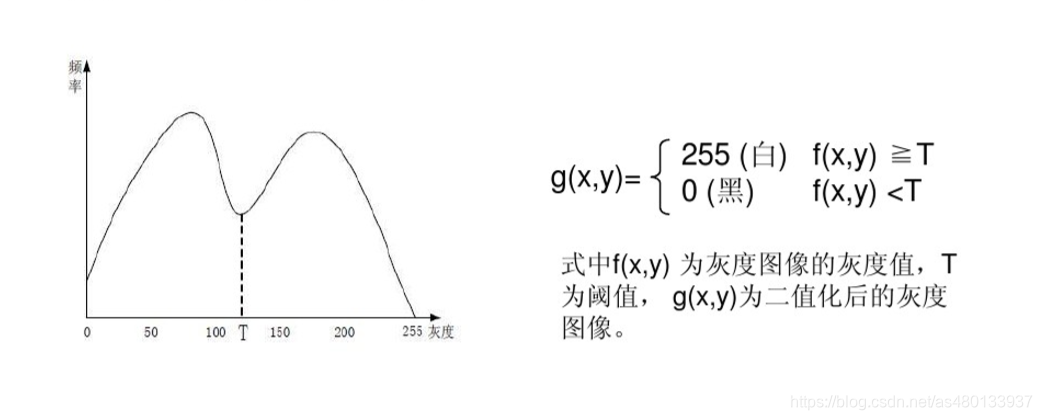
3.双峰法

介绍：如果图像灰度直方图呈明显的双峰状，则选取双峰间的最低谷出作为图像分割的阈值所在。，如下图，以T为阈值进行二值化分，可以将目标和背景分割开。

在一些简单的图像中，物体的灰度分布比较有规律，背景与各个目标在图像的直方图各自形成一个波峰，即区域与波峰一一对应，每两个波峰之间形成一个波谷。那么，选择双峰之间的波谷所代表的灰度值T作为阈值，即可实现两个区域的分割。如下图所示。

代码实现：

int GetIntermodesThreshold(int* HistGram)
    {        int Y, Iter = 0, Index;        double* HistGramC = new double\[256\];           // 基于精度问题，一定要用浮点数来处理，否则得不到正确的结果
        double* HistGramCC = new double\[256\];          // 求均值的过程会破坏前面的数据，因此需要两份数据
        for (Y = 0; Y < 256; Y++)
        {
            HistGramC\[Y\] = HistGram\[Y\];
            HistGramCC\[Y\] = HistGram\[Y\];
        }        // 通过三点求均值来平滑直方图
        while (IsDimodal(HistGramCC) == false)                                                  // 判断是否已经是双峰的图像了      
        {
            HistGramCC\[0\] = (HistGramC\[0\] + HistGramC\[0\] + HistGramC\[1\]) / 3;                   // 第一点
            for (Y = 1; Y < 255; Y++)
                HistGramCC\[Y\] = (HistGramC\[Y - 1\] + HistGramC\[Y\] + HistGramC\[Y + 1\]) / 3;       // 中间的点
            HistGramCC\[255\] = (HistGramC\[254\] + HistGramC\[255\] + HistGramC\[255\]) / 3;           // 最后一点
            memcpy(HistGramCC, HistGramC, 256 * sizeof(double));         // 备份数据，为下一次迭代做准备
            Iter++;            if (Iter >= 10000) return -1;                                                       // 似乎直方图无法平滑为双峰的，返回错误代码
        }// 阈值为两峰值的平均值
        int* Peak = new int\[2\];        for (Y = 1, Index = 0; Y < 255; Y++)            if (HistGramCC\[Y - 1\] < HistGramCC\[Y\] && HistGramCC\[Y + 1\] < HistGramCC\[Y\]) Peak\[Index++\] = Y - 1;        return ((Peak\[0\] + Peak\[1\]) / 2);
    }    bool IsDimodal(double* HistGram)       // 检测直方图是否为双峰的
    {        // 对直方图的峰进行计数，只有峰数位2才为双峰 
        int Count = 0;        for (int Y = 1; Y < 255; Y++)
        {            if (HistGram\[Y - 1\] < HistGram\[Y\] && HistGram\[Y + 1\] < HistGram\[Y\])
            {
                Count++;                if (Count > 2) return false;
            }
        }        if (Count == 2)            return true;        else
            return false;
    }

Python代码：

#coding:utf-8import cv2import numpy as npfrom matplotlib import pyplot as plt

image = cv2.imread("E:/python/cv/2ModeMethod/test.jpg")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

plt.subplot(131), plt.imshow(image, "gray")
plt.title("source image"), plt.xticks(\[\]), plt.yticks(\[\])
plt.subplot(132), plt.hist(image.ravel(), 256)
plt.title("Histogram"), plt.xticks(\[\]), plt.yticks(\[\])
ret1, th1 = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
plt.subplot(133), plt.imshow(th1, "gray")
plt.title("2-Mode Method"), plt.xticks(\[\]), plt.yticks(\[\])
plt.show()

缺点：当不同区域（即目标）之间的灰度分布有一定的重叠时，双峰法的效果就很差，也就是说，图像为双峰时才能用双峰法

上述代码已经给出判断双峰图的代码

4最佳迭代法

迭代法图像二值化的算法思想是：首先，初始化一个阈值Th，然后按照某种策略通过迭代不断更新这一阈值，直到满足给定的约束条件为止。

迭代法是基于逼近的思想，迭代阈值的获取步骤可以归纳如下：

（1）求出图象的最大灰度值和最小灰度值，分别记为gl和gu，令初始阈值为：

                  ![](https://imgconvert.csdnimg.cn/aHR0cHM6Ly9pbWFnZXMwLmNuYmxvZ3MuY29tL2Jsb2cvMzQ5MjkzLzIwMTMwOS8wNzExMDA1OS01ODQ5YmYzM2IwYjE0NTRkODk0NjkwZGIzODU1YTIwMi54LXBuZw?x-oss-process=image/format,png)

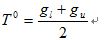
(2) 根据阈值T0将图象分割为前景和背景，分别求出两者的平均灰度值Ab和Af:

　　 　　　　

(3) 令

                    ![](https://imgconvert.csdnimg.cn/aHR0cHM6Ly9pbWFnZXMwLmNuYmxvZ3MuY29tL2Jsb2cvMzQ5MjkzLzIwMTMwOS8wNzExMDcxMS04MDIwZGIyNDRmMTY0OGUyYTM3MjUyM2FmNDkxYzY5Ny54LXBuZw?x-oss-process=image/format,png)

如果Tk=Tk+1,则取Tk为所求得的阈值，否则，转2继续迭代

MATALB代码实现：

>> clear all

%读入图像

I=imread('D:\\Administrator\\My Pictures\\Lenagray.bmp');

%计算灰度的最小值和最大值

tmin=min(I(:));

tmax=max(I(:));

%设定初始阈值

th=(tmin+tmax)/2;

%定义开关变量，用于控制循环次数

ok=true;

%迭代法计算阈值while ok

   g1=I>=th;

   g2=I<=th;

   u1=mean(I(g1));

   u2=mean(I(g2));

   thnew=(u1+u2)/2;

   %设定两次阈值的比较，当满足小于1时，停止循环

   ok=abs(th-thnew)>=1;

   th=thnew;

end

th=abs(floor(th));

%阈值分割

J=im2bw(I,th/255);

%结果显示

figure(1);

imshow(I);title('原始图像');

figure(2);

str=\['迭代分割：阈值Th=',num2str(th)\];

imshow(J);

title(str);

代码实现：

 public static int GetIterativeBestThreshold(int\[\] HistGram)
    {        int X, Iter = 0;        int MeanValueOne, MeanValueTwo, SumOne, SumTwo, SumIntegralOne, SumIntegralTwo;        int MinValue, MaxValue;        int Threshold, NewThreshold;        for (MinValue = 0; MinValue < 256 && HistGram\[MinValue\] == 0; MinValue++) ;        for (MaxValue = 255; MaxValue > MinValue && HistGram\[MinValue\] == 0; MaxValue--) ;        if (MaxValue == MinValue) return MaxValue;          // 图像中只有一个颜色             
        if (MinValue + 1 == MaxValue) return MinValue;      // 图像中只有二个颜色

        Threshold = MinValue;
        NewThreshold = (MaxValue + MinValue) >> 1;        while (Threshold != NewThreshold)    // 当前后两次迭代的获得阈值相同时，结束迭代    
        {
            SumOne = 0; SumIntegralOne = 0;
            SumTwo = 0; SumIntegralTwo = 0;
            Threshold = NewThreshold;            for (X = MinValue; X <= Threshold; X++)         //根据阈值将图像分割成目标和背景两部分，求出两部分的平均灰度值      
            {
                SumIntegralOne += HistGram\[X\] * X;
                SumOne += HistGram\[X\];
            }
            MeanValueOne = SumIntegralOne / SumOne;            for (X = Threshold + 1; X <= MaxValue; X++)
            {
                SumIntegralTwo += HistGram\[X\] * X;
                SumTwo += HistGram\[X\];
            }
            MeanValueTwo = SumIntegralTwo / SumTwo;
            NewThreshold = (MeanValueOne + MeanValueTwo) >> 1;       //求出新的阈值
            Iter++;            if (Iter >= 1000) return -1;
        }        return Threshold;
    }

5百分比阈值（P-Tile法）

p-tile算法是一种基于灰度直方图统计的的自动阈值选择算法，该算法需要基于一定的先验条件—背景与目标所占的面积比P%。
该算法选择阈值的原则是，依次累积灰度直方图，直到该累积值大于或等于前景图像（目标）所占面积，此时的灰度级即为所求的阈值

代码实现：

  //HistGram灰度图像的直方图
 //Tile背景在图像中所占的面积百分比
    int GetPTileThreshold(int* HistGram, int Tile)
    {        int Y, Amount = 0, Sum = 0;        for (Y = 0; Y < 256; Y++) Amount += HistGram\[Y\];        //  像素总数
         for (Y = 0; Y < 256; Y++)
        {
            Sum = Sum + HistGram\[Y\];            if (Sum >= Amount * Tile / 100) return Y;
        }        return -1;
    }

缺点：该方法简单高效，但是对于先验概率难于估计的图像却无能为力。。条件很苛刻，大部分情况下都用不上

6.Niblack二值化算法

Niblack二值化算法是比较简单的局部阈值方法，阈值的计算公式是T = m + k*v，其中m为以该像素点为中心的区域的平均灰度值，v是该区域的标准差，k是一个修正系数

它根据以像素点为中心的邻域内的点的情况为此像素计算阈值。下面是每个像素阈值的计算公式，m是均值，s是标准差

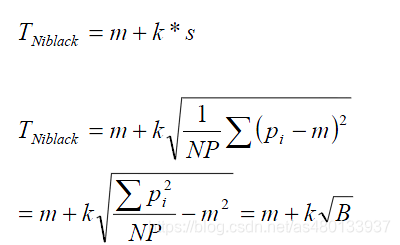
MATALB代码：

function g=segNiBlack(f,w2,k)
% segmentation method using Niblack thresholding method
% input: w2 is the half width of the window
 
w = 2*w2 + 1;
window = ones(w, w);
% compute sum of pixels in WxW window
sp = conv2(f, window, 'same');
% convert to mean
n = w^2;            % number of pixels in window
m = sp / n;
% compute the stdif k ~= 0
    % compute sum of pixels squared in WxW window
    sp2 = conv2(f.^2, window, 'same');
    % convert to std
    var = (n*sp2 - sp.^2) / n / (n-1);
    s = sqrt(var);  
    % compute Niblack threshold
    t = m + k * s;else
    t = m;
end
g=f<t;
 
end

C代码：

void NiBlack(BYTE \*image\_in, BYTE \*image\_out, int xsize, int ysize){/*////////////////////////////////////////////////////////////////////
// 作者：杨魁
//参数列表：
//image_in            输入图像的指针
//image_out        输出图像的指针
//xsize                图像的宽
//ysize                图像的高
////////////////////////////////////////////////////////////////////*/
 int sum = 0;int i, j, h, k;;//用于循环int Average = 0;//平均值int num = 0;//用于自加int w\_size = 7;//窗口大小为2\*w\_size+1int Area = (2 \* w\_size + 1)*(2 * w\_size + 1);int \*d = (int \*)malloc(sizeof(int)*Area);//数组空间int T = 0;//阈值int S = 0;//标准差
 for (j = w\_size; j < ysize - w\_size; j++)
{    for (i = w\_size; i < xsize - w\_size; i++)
    {
        sum = 0;
        num = 0;        for (h = 0; h < 2 * w_size + 1; h++)
        {            for (k = 0; k < 2 * w_size + 1; k++)
            {
                d\[num++\] = GetGray(image\_in, xsize, i + w\_size - k, j + w_size - h);        //求area领域内的像素值
            }
        }        for (h = 0; h <Area; h++)
        {
            sum += d\[h\];//求总和
        }
        Average = sum / Area;
        sum = 0;        for (h = 0; h < Area; h++)
        {
            sum += (d\[h\] * d\[h\]);
        }
        S = sqrt((float)sum);
        S = S / Area;
         T = Average + 0.05*S;//确定阈值
        *(image\_out + j \*xsize + i) = \*(image\_in + j *xsize + i) > T ? 255 : 0;
    }
}free(d);

C

/// <summary>  /// 快速的二维数组元素局部窗口求和程序  /// </summary>  /// <param name="array"> 输入二维数组</param>   /// <param name="winR">窗口半径</param>  /// <returns>输出结果</returns>  /// <summary>  public static int\[,\] LocalSum_Fast(byte\[,\] array, int winR)  
{  
    int width = array.GetLength(0);  
    int height = array.GetLength(1);  
    int\[,\] temp = new int\[width, height\];//保存中间结果的数组  
    int\[,\] sum = new int\[width, height\];  
  
    //不考虑边界情况，  
    //水平方向：winR行至width-winR行，  
    //垂直方向：winR列至width-winR列  
  
    //对起始行winR在垂直方向求线性和  
    for (int x = winR; x < width - winR; x++)  
    {  
        for (int k = -winR; k <= winR ; k++)  
        {  
            temp\[x, winR\] += array\[x, winR + k\];  
        }  
    }  
    //从winR+1行至末尾行height-winR，依次基于前一行的求和结果进行计算。  
    for (int y = winR + 1; y < height - winR; y++)  
    {  
        for (int x = winR; x < width - winR; x++)  
        {  
            temp\[x, y\] = temp\[x, y - 1\] + array\[x, y + winR\]   
                         - array\[x, y - 1 - winR\];  
        }  
    }  
      
    //基于保存的垂直方向求和结果，进行水平方向求和  
    //对起始列winR在水平方向求线性和  
    for (int y = winR; y < height - winR; y++)  
    {  
        for (int k = -winR; k <= winR ; k++)  
        {  
            sum\[winR, y\] += temp\[winR + k, y\];  
        }  
    }  
    //从winR+1列至末尾列height-winR，依次基于前一列的求和结果进行计算。  
    for (int x = winR + 1; x < width - winR; x++)  
    {  
        for (int y = winR; y < height - winR; y++)  
        {  
            sum\[x, y\] = sum\[x - 1, y\] + temp\[x + winR, y\]   
                        - temp\[x - winR - 1, y\];  
        }  
    }  
    //运算完成，输出求和结果。  
    return sum;  
}

7.bernsen二值化

bernsen算法的中心思想：

先人为设定两个值S与TT(Bemsen最初设S为15，TT设为128)，计算以图像中任意像素尸为中心的大小为k×k窗口内的所有像素的最大值M与最小值N，两者的均值T，如果朋M-N大于S，则当前P的阈值为T；若小于S，则表示该窗口所在区域灰度级灰度级差别较小，那么窗口在目标区或在背景区，再判断T与TT的关系，若T>TT则当前点灰度值为255，否则当前点灰度值为0。

改进的bernsen算法：

1.消除个别灰度特异点，设采用的阈值为T1。

T1的取值满足：

A为图像的总像素个数

代码实现：

int getThreshBernsen(IplImage *src)
    {
        uchar num\[256\];        int w = src->width;        int h = src->height;        int s = src->widthStep;        int T1 = 0;        int pix = 0;        int a = w * h;        memset(num, 0, 256);        //统计灰度值的个数
        for(int i=0; i<=255; i++)
        {            for(int j=1; j<= h; j++)
            {                for(int m=1; m<= w; m++)
                {                    if(((uchar*)src->imageData + j*s)\[m\] == i)
                    {
                        num\[i\] = num\[i\] + 1;
                    }
                }
            }

        }        for(int i=255; i>=0; i--)
        {
            pix = pix + num\[i\];            if(pix >= (0.1*a))
            {
                T1 = i;                break;
            }
        }        cout << T1 << endl;        return T1;

    }

二值化的方法有很多，基于每个人来说都会有着适合自己的方法，这里我们只介绍上述几种主流方法，正常使用已经足以，方法不在于多，而在于精，可能你用一种方法就很完美，也可能要不断修改，找到最适合的，图像处理好才是王道。

参考：

ttps://www.cnblogs.com/Imageshop/p/3307308.html
https://blog.csdn.net/liuzhuomei0911/article/details/51440305
https://blog.csdn.net/jinzhichaoshuiping/article/details/51480520
https://www.cnblogs.com/naniJser/archive/2012/12/12/2814324.html
https://blog.csdn.net/wu\_lian\_nan/article/details/69371720
https://blog.csdn.net/zyzhangyue/article/details/45841121

还有一些参考较少的文献，这里就不罗列了，写这个用到参考文献实在太多，抱歉抱歉

整理实属不易，点个赞再走呗！