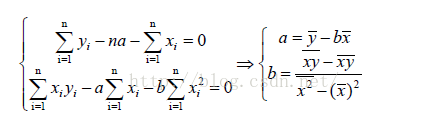智能车学习----最小二乘法求拟合曲线(中线)的斜率

最小二乘法：

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最 小，简单来说，就是通过最小化误差的平方和，使得拟合对象无限接近目标对象，这就是最小二乘的核心思想。最小二乘法还可用于曲线拟合。

在此先列举一下最小二乘家族成员。最小二乘法直线拟合，最小二乘法多项式（曲线）拟合，机器学习中线性回归的最小二乘法，系统辨识中的最小二乘辨识法，参数估计中的最小二乘法，等等

这里我们要说的是最小二乘法拟合曲线的斜率。

拟合直线作用：

在我们做一些处理的时候，得到的数据可能是一些离散的点，而我们往往希望得到一个连续的函数（也就是拟合直线）或者更加密集的离散方程与已知数据相吻合，这过程就叫做拟合，

以智能车为例把，我们平时得到的中线，可以说就是一些离散的点，它不是一条顺滑的曲线，而我们的拟合直线，则使用在中线和各种赛道元素补线上，在用中线做偏差处理时，将中线拟合一下，得到的斜率偏差则是会更加精确，在一些特殊的赛道元素，如环岛，我们可以用最小二乘法做补线处理，

概念与公式：

说到最小二乘法，可能有的同学说没学过，但是我们给出公式应该同学们会说：哦！原来是他啊。

推导：

即为：

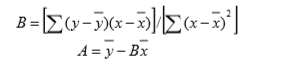
最小二乘法多项式直线拟合，就是根据给定的点，用计算的方法求出最佳的 a(斜率) 和 b（截距）。显然，关键是如何求出最佳的 a 和 b。

相信各位高中都已经学过了，下面我们给出计算中线斜率的代码

/************************************线性回归计算中线斜率************************************/// y = Ax+Bint regression(int startline,int endline){  
  int i=0,SumX=0,SumY=0,SumLines = 0; 
  float SumUp=0,SumDown=0,avrX=0,avrY=0,B,A;
  SumLines=endline-startline;   // startline 为开始行， //endline 结束行 //SumLines
 
  for(i=startline;i<endline;i++)     
  { 
    SumX+=i;       
    SumY+=Middle\_black\[i\];    //这里Middle\_black为存放中线的数组
  }         
  avrX=SumX/SumLines;     //X的平均值
  avrY=SumY/SumLines;     //Y的平均值       
  SumUp=0;      
  SumDown=0;  
  for(i=startline;i<endline;i++)   
  {       
    SumUp+=(Middle_black\[i\]-avrY)*(i-avrX);    
    SumDown+=(i-avrX)*(i-avrX);    
  }    
  if(SumDown==0) 
    B=0;  
  else 
    B=(int)(SumUp/SumDown);       
    A=(SumY-B*SumX)/SumLines;  //截距
    return B;  //返回斜率}

看代码很容易可以理解。

对于斜率的使用，个人是将他与误差结合起来使用，效果还输不错的

那么，用最小二乘法除了拟合中线斜率之外，我们还可以用斜率进行补线操作，以及用最小二乘法预估赛道边界，等等

这里我们暂时不做阐述，之后博文会更新，